Calculo Diferencial
UNIDAD 1. NÚMEROS REALES.
1.1. Recta numérica.
En matemáticas, un número natural (designado por ℕ) es cualquiera de los números que se usan para contar los elementos de un conjunto.
Es todo número perteneciente a la serie ℕ = {0, 1, 2, 3, 4, …} formada por todos los números que, a partir del cero (o ausencia de elemento), el uno inicia y sin término medio.
.Los números naturales en la vida cotidiana:
Cuando el hombre tuvo la necesidad de ordenar conjuntos y comparar la cantidad de elementos que los conformaban aparecieron los números naturales.
Para poder negociar y ordenar elementos, el hombre tuvo la necesidad de representar las cantidades de lo que poseía y así saber de qué disponía exactamente. De ahí surgió la necesidad de crear símbolos que representaran esas cantidades.
Por ejemplo, si alguien sabía la cantidad de gallinas que tenía en su finca, podría establecer del mismo modo la cantidad de días que podría alimentar a su familia.
Es por esta necesidad que el hombre crea lo que hoy conocemos como números naturales. Ellos son los primeros que surgen en las distintas civilizaciones debido a que contar y ordenar elementos son las tareas más elementales en el tratamiento de las cantidades.
Los números naturales son aquellos que nos permiten representar la cantidad de elementos que tiene un conjunto.
Debido a que este conjunto de números es conocido en todas las culturas, se ha creado un símbolo especial para identificarlo. Usaremos el símbolo N para representar el conjunto de los números naturales. Así, cuando veas el símbolo N en un libro de matemáticas, o en alguna clase, ya sabrás a qué se refiere.
Como te podrás imaginar, el conjunto de los números naturales es infinito. ¿Te has preguntado cuál es el último numero natural? No hay, sencillamente no existe un número natural que sea más grande que todos los demás, cada vez que pienses en uno muy grande, podrás encontrar muchos que sean más grandes que él.
Números naturales:
- Positivos
- Negativos
- Fraccionarios
- Decimales
- Racionales
- Irracionales
.Números reales:
En matemáticas,el conjunto de los números reales (denotado por ℝ) incluye tanto a los números racionales (positivos, negativos y el cero) como a los números irracionales; y en otro enfoque, trascendentes y algebraicos. Los irracionales y los trascendentes (1970) no se pueden expresar mediante una fracción de dos enteros con denominador no nulo; tienen infinitas cifras decimales a periódicas, tales como: √5, π, el número real log2, cuya trascendencia fue enunciada por Euler en el siglo XVIII.1
Los números reales pueden ser descritos y construidos de varias formas, algunas simples aunque carentes del rigor necesario para los propósitos formales de matemáticas y otras más complejas pero con el rigor necesario para el trabajo matemático formal.
.Tipos de números reales:
Racionales e irracionales[editar]
Un número real puede ser un número racional o un número irracional. Los números racionales son aquellos que pueden expresarse como el cociente de dos números enteros, tal como 3/4, -21/3, 5, 0, 1/2, mientras que los irracionales son todos los demás. Los números racionales también pueden describirse como aquellos cuya representación decimal es eventualmente periódica, mientras que los irracionales tienen una expansión decimal aperiódica:
- Ejemplos
- 1/4 = 0,250000... Es un número racional puesto que es periódico a partir del tercer número decimal.
- 5/7 = 0,7142857142857142857.... Es racional y tiene un período de longitud 6 (repite 714285).
![\frac{\sqrt[3]{7}+1}{2}=1\text{,}456465591386194\ldots](https://upload.wikimedia.org/math/f/9/e/f9e0469fdfd9e2047c07e37776ca52da.png) es irracional y su expansión decimal es aperiódica.
es irracional y su expansión decimal es aperiódica.
El conjunto de los números racionales se designa mediante  .
.
 .
.Algebraicos y trascendentes
Otra forma de clasificar los números reales es en algebraicos y trascendentes. Un número es algebraico si existe un polinomio de coeficientes racionales que lo tiene por raíz y es trascendente en caso contrario. Obviamente, todos los números racionales son algebraicos: si  es un número racional, con p entero y q natural, entonces es raíz de la ecuación qx=p. Sin embargo, no todos los números algebraicos son racionales.
es un número racional, con p entero y q natural, entonces es raíz de la ecuación qx=p. Sin embargo, no todos los números algebraicos son racionales.
 es un número racional, con p entero y q natural, entonces es raíz de la ecuación qx=p. Sin embargo, no todos los números algebraicos son racionales.
es un número racional, con p entero y q natural, entonces es raíz de la ecuación qx=p. Sin embargo, no todos los números algebraicos son racionales.- Ejemplos
- El número
![\frac{\sqrt[3]{7}+1}{2}](https://upload.wikimedia.org/math/2/0/a/20adde2b96dd019de6c9bf35f73f85f4.png) es algebraico puesto que es una raíz del polinomio
es algebraico puesto que es una raíz del polinomio 
- Un ejemplo de número trascendente es

El conjunto de los números algebraicos se designa mediante  .
.
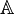 .
.Computables e irreductibles
Un número real se dice computable si tiene una complejidad de Kolmogórov finita, es decir, si puede escribirse un programa informático de extensión finita que genere los dígitos de dicho número. Si un número real no es computable se dice irreductible. Una definición de número irreductible es:
El conjunto de números reales computables se designa por  . Obviamente los racionales y los algebraicos son números computables. De hecho se tiene la siguiente inclusión:
. Obviamente los racionales y los algebraicos son números computables. De hecho se tiene la siguiente inclusión:
 . Obviamente los racionales y los algebraicos son números computables. De hecho se tiene la siguiente inclusión:
. Obviamente los racionales y los algebraicos son números computables. De hecho se tiene la siguiente inclusión:
Además se tiene que todos estos conjuntos son numerables:
Esto implica que el conjunto de todos los números computables es un conjunto de medida nula.
ejemplo:
.Esquemas de dichos números.

.Su clasificaciones.
.Propiedades de los números reales.
como también para poder hacer soluciones a los problemas matemáticos que se nos pueda dificultar.
asi también los podemos observar y comprender mejor, como obtener soluciones y como es su representación.
en estas tenemos los axiomas las cuales son las siguientes:
asociadas suma: (a+b)+c = a+(b+c)
conmutativa suma: a+b=b+a
conmutataiva multiplicacion: a*b= b*a
distributiva a(b+c)=ab+ac
elemento neutro aditivo: a+0=a
elemento neutro multiplicativo: a*1=a
elementoinverso aditivo: a+(-a)=a
elemento inverso multiplicativo: a*a-1= 1 o (a* 1/a 1)
ejemplos:
Propiedad
|
Operación
|
Definición
|
Que dice
|
Ejemplo
|
| Conmutativa | Suma Multiplicación | a+b = b+a ab = ba | El orden al sumar o multiplicar reales no afecta el resultado. | 2+8 = 8+2 5(-3) = ( -3)5 |
Propiedad
|
Operación
|
Definición
|
Que dice
|
Ejemplo
|
| Asociativa | Suma Multiplicación | a+(b+c)=(a+b)+c a(bc) = (ab)c | Puedes hacer diferentes asociaciones al sumar o multiplicar reales y no se afecta el resultado. | 7+(6+1)=(7+6)+1 -2(4x7)= (-2x4)7 |
Propiedad
|
Operación
|
Definición
|
Que dice
|
Ejemplo
|
| Identidad | Suma Multiplicación | a + 0 = a a x 1= a | Todo real sumado a 0 se queda igual; el 0 es laidentidad aditiva. Todo real multiplicado por 1 se queda igual; el 1es la identidad multiplicativa. | -11 + 0 = -11 17 x 1 = 17 |
Propiedad
|
Operación
|
Definición
|
Que dice
|
Ejemplo
|
| Inversos | Suma Multiplicación | a + ( -a) = 0 | La suma de opuestos es cero. El producto de recíprocos es 1. | 15+ (-15) = 0 |
Propiedad
|
Operación
|
Definición
|
Que dice
|
Ejemplo
|
| Distributiva | Suma respecto a Multiplicación | a(b+c) = ab + ac | El factor se distribuye a cada sumando. | 2(x+8) = 2(x) + 2(8) |
.Subconjuntos de numeros reales a través de intervalos
intervalo
Un subconjunto de la recta real se llama intervalo, y contiene a todos los números reales que están comprendidos entre dos cualesquiera de sus elementos.
Geométrica mente los intervalos corresponden a segmentos de recta, semirrectas o la misma recta real.
Los intervalos de números correspondientes a segmentos de recta son intervalos finitos, los intervalos correspondientes a semirrectas y a la recta real son intervalos infinitos.
Los intervalos finitos pueden ser cerrados, abiertos o semiabiertos.
Sean a y b dos números reales tales que a < b.
Intervalo cerrado
Es el conjunto de números reales formado por a, b y todos los comprendidos entre ambos.
[a, b] = { x / a £ x £ b}
Intervalo abierto
Es el conjunto de los números reales comprendidos entre a y b.
(a, b) = {x / a < x < b}
Intervalo semiabierto a izquierda (o semicerrado a derecha)
Es el conjunto de números reales formado por b y los números comprendidos entre a y b.
(a, b] = {x / a < x £ b}
Es el conjunto de números reales formado por a y los números comprendidos entre a y b.
[a, b) = { x / a £ x < b}
Intervalos infinitos
[a, +¥) = { x / x ³ a} (a, +¥) = { x / x > a}
(-¥ , b] = { x / x £ b} (-¥ , b) = { x / x < b}
(-¥ , +¥ ) = R
Ejemplo. Interprete gráficamente los intervalos: a) [-2, 3] b) (1, 4) c) (0, 5] d) [1, +¥ ) e) (-¥ , 3)
.Otros ejemplos:
b) El intervalo (1, 4) corresponde a todos los números reales entre 1 y 4. Es abierto pues no incluye a los extremos. Gráficamente:
c) El intervalo (0, 5] comprende todos los números reales entre 0 y 5 incluyendo el extremo 5. Se trata de un intervalo semiabierto a izquierda o bien semicerrado a derecha. Su gráfica es:
d) El intervalo [1, +¥ ) es infinito y comprende todos los números reales mayores o iguales a 1. Gráficamente:
e) El intervalo (-¥, 3) es infinito y comprende todos los números reales menores que 3. Su gráfica es:
en resumen de todo esto:
| Nombre del intervalo | Notación conjuntista | Notación de intervalos | Representación gráfica |
| Abierto | {x / a < x < b} | (a, b) | |
| Semicerrado a derecha | {x / a < x £ b} | (a, b] | |
| Semicerrado a izquierda | { x / a £ x < b} | [a, b) | |
| Cerrado |
{ x / a £ x £ b}
| [a, b] | |
| Infinito abierto a izquierda | { x / x > a} | (a, +¥ ) | |
| Infinito cerrado a izquierda | { x / x ³ a} | [a, +¥ ) | |
| Infinito abierto a derecha | { x / x < b} | (-¥ , b) | |
Infinito cerrado a derecha
| { x / x £ b} | (-¥ , b] | |
| Infinito | R | (-¥ , +¥ ) |
1) Escriba como intervalo el conjunto definido sobre la recta real.
| a) | b) |
| c) | d) |
| e) | f) |
respuestas:
| a) [ -3, 2] | b) [4, 8) | c) (-¥, -2) | d) (-5, 2) | e) [1, +¥ ) | f) (-2, 4] |
2) Escriba, si es posible, como intervalo o unión de intervalos los siguientes conjuntos de números reales:
| a) A = { x / 5 < x < 9} | b) B = { x / -1 £ x £ 3} |
| c) C = { x / x < -2 Ú x > 2} | d) D = { x / -4 < x < 2 Ù x ¹ -1} |
respuestas:
| a) (5 , 9) | b) [–1, 3] | c) (-¥ , -2) È (2, +¥ ) | d) (–4, –1)È (–1, 2 | ||
Desigualdades con intervalos.


No hay comentarios:
Publicar un comentario