Calculo Diferencial
UNIDAD 2.
En matemáticas, se dice que una magnitud o cantidad es función de otra si el valor de la primera depende exclusivamente del valor de la segunda. Por ejemplo el área A de un círculo es función de su radio r: el valor del área es proporcional al cuadrado del radio, A = π·r2. Del mismo modo, la duración T de un viaje de tren entre dos ciudades separadas por una distancia d de 150 km depende de la velocidad v a la que este se desplace: la duración es inversamente proporcional a la velocidad, d / v. A la primera magnitud (el área, la duración) se la denomina variable dependiente, y la cantidad de la que depende (el radio, la velocidad) es la variable independiente.
En análisis matemático, el concepto general de función, aplicación o mapeo se refiere a una regla que asigna a cada elemento de un primer conjunto un único elemento de un segundo conjunto (correspondencia matemática). Por ejemplo, cada número entero posee un único cuadrado, que resulta ser un número natural (incluyendo el cero):
| ... | −2 → +4, | −1 → +1, | ±0 → ±0, | |
| +1 → +1, | +2 → +4, | +3 → +9, | ... |
Esta asignación constituye una función entre el conjunto de los números enteros Z y el conjunto de los números naturales N. Aunque las funciones que manipulan números son las más conocidas, no son el único ejemplo: puede imaginarse una función que a cada palabra del español le asigne su letra inicial:
| ..., | Estación → E, | Museo → M, | Arroyo → A, | Rosa → R, | Avión → A, | ... |
Esta es una función entre el conjunto de las palabras del español y el conjunto de las letras del alfabeto español.
La manera habitual de denotar una función f es:
- f: A → B
- a → f(a),
- donde A es el dominio de la función f, su primer conjunto o conjunto de partida; y B es el codominio de f, su segundo conjunto o conjunto de llegada. Por f(a) se denota la regla o algoritmo para obtener la imagen de un cierto objeto arbitrario a del dominio A, es decir, el (único) objeto de B que le corresponde. En ocasiones esta expresión es suficiente para especificar la función por completo, infiriendo el dominio y codominio por el contexto. En el ejemplo anterior, las funciones «cuadrado» e «inicial», llámeseles f y g, se denotarían entonces como:
- f: Z → N
- k → k2, o sencillamente f(k) = k2;
- g: V → A
- p → Inicial de p;
si se conviene V = {Palabras del español} y A = {Alfabeto español}.Una función puede representarse de diversas formas: mediante el citado algoritmo o ecuaciones para obtener la imagen de cada elemento, mediante una tabla de valores que empareje cada valor de la variable independiente con su imagen —como las mostradas arriba—, o como una gráfica que dé una imagen de la función. - Dominio del la función.
- El dominio (conjunto de definición o conjunto de partida) de una función
 es el conjunto de existencia de ella misma, es decir, los valores para los cuales la función está definida. Es el conjunto de todos los objetos que puede transformar, se denota
es el conjunto de existencia de ella misma, es decir, los valores para los cuales la función está definida. Es el conjunto de todos los objetos que puede transformar, se denota  o bien
o bien 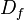 . En
. En  se denomina dominio a un conjunto conexo, abierto y cuyo interior no sea vacío.Por otra parte, el conjunto de todos los resultados posibles de una función dada se denomina imagen de esa función.
se denomina dominio a un conjunto conexo, abierto y cuyo interior no sea vacío.Por otra parte, el conjunto de todos los resultados posibles de una función dada se denomina imagen de esa función. Rango de la función.
- Se denomina rango o recorrido de una función al conjunto de los valores reales que toma la variable y o f(x).Conjunto inicial Conjunto finalDominio Rango o recorrido o conjunto imagen
- Parte de la función.
Parte de la función
Lo que sale (el rango) depende de lo que pones (el dominio), pero TÚ defines el dominio.De hecho el dominio es una parte esencial de la función. Un dominio diferente da una función diferente.Ejemplo: una simple función como f(x) = x2 puede tener dominio (lo que entra) los números de contar {1,2,3,...}, y el rango será entonces el conjunto {1,4,9,...}Y otra función g(x) = x2 puede tener como dominio los enteros {...,-3,-2,-1,0,1,2,3,...}, entonces el rango será el conjunto {0,1,4,9,...}Condominio y rango
El codominio y el rango tienen que ver con la salida, pero no son exactamente lo mismo.El codominio es el conjunto de valores que podrían salir.El rango es el conjunto de valores que realmente salen.Ejemplo: puedes definir una función f(x)=2x con dominio y codominio los enteros (porque tú lo eliges así).Pero si lo piensas, verás que el rango (los valores que salen de verdad) son sólo los enteros pares.Así que el codominio son los enteros (lo has elegido tú) pero el rango son los enteros pares.Así que rango es un subconjunto del codominio.¿Por qué los dos? Bueno, a veces no conoces exactamente el rango (porque la función es complicada o no es conocida del todo), pero sabes el conjunto en el que está (como los enteros o los reales). Así que defines el codominio y sigues trabajando.La importancia del codominio
Déjame que te haga una pregunta: ¿la raíz cuadrada es una función?Si tú dices que el codominio (las salidas posibles) es el conjunto de los números reales, ¡entonces la raíz cuadrada no es una función! ... ¿te sorprende?La razón es que podría haber dos respuestas para una entrada, por ejemplo f(9) = 3 o -3Una función debe ser univaluada. No puede dar 2 resultados para el mismo valor de entrada. ¡Por ejemplo "f(2) = 7 o 9" no está bien!Pero se puede arreglar simplemente limitando el codominio a los números reales no negativos.√De hecho, el símbolo radical (como en √x) siempre significa la raíz cuadrada positiva (la principal), así que √x es una función porque su codominio es correcto.Así que el codominio que elijas puede afectar el que algo sea o no una función.Notación
A los matemáticos no les gusta escribir muchas palabras cuando unos pocos símbolos hacen el mismo trabajo. Así que hay maneras de decir que "el dominio es", "el codominio es", etc.Esta es la mejor manera que conozco:Esto dice que la función "f" tiene dominio "N" (los números naturales), y también codominio "N".y esto dice que la función "f" toma "x" y devuelve "x2"- Funciones.
- Tipos de funciones.
- Representación de funciones.
Gráfica de una función
La gráfica de una función está formada por el conjunto de puntos (x, y) cuando x varía en el dominio D.- Dada una función
f(x) definidaf:Xx⟶⟼Yf(x)=y
definimos la gráfica de esta función como el conjunto de puntos:{(x,y)∈X×Y | y=f(x)} o también los pares de puntos(x,f(x)) . Estos puntos se pueden representar con coordenadas cartesianas en el planoXY formándose así el dibujo de la gráfica de la funciónf(x) .
Ejemplo
Tomemos la funciónf(x)=x3 . Su gráfica vendrá dada por el conjunto de puntos{(x,f(x))}={(x,x3)} variando el valor dex .Si lo representamos obtenemos el dibujo:Pero, ¿Cómo se representa una gráfica? Para poder explicarlo debemos introducir antes el concepto de dominio e imagen de una función.En una funciónf(x) distinguimos dos conjuntos: uno es el conjunto de donde tomamos valores para evaluar la función (los posibles valores dex ) y el otro es el conjunto formado por los diferentes valores que alcanza la funciónf(x) .Entonces, definimos:- Dominio de una función como el conjunto de valores donde evaluaremos la función. Se denota como:
Dom(f) . - Imagen de una función como el conjunto de valores obtenidos por la función. Se denota como:
Im(f) .
Fijémonos que cuando notamos una función como:f:Xx⟶⟼Yf(x)=y
el conjuntoX es el dominio, puesto que tomaremos los valores dex de dentro de éste y la imagen estaría dentro del conjuntoY .Veámoslo mejor con algunos ejemplos:Ejemplo
La funciónf(x)=x tiene como dominio toda la recta real, puesto que podemos evaluarla en cualquier punto, y tiene como imagen la misma recta, ya que la función es la identidad.Por lo tanto escribiremos:Dom(f)=R=(−∞,∞) Im(f)=R=(−∞,∞) Ejemplo
La función téf(x)=x2 tiene como dominio también toda la recta real (podemos evaluarla en cualquier punto) y no obstante, al ser la función "elevar al cuadrado", sólo obtenemos valores positivos. Por consiguiente su imagen será la semirecta real positiva incluyendo el cero.Por lo tanto escribiremos:Dom(f)=R=(−∞,∞) Im(f)=[0,∞) Podemos observar que el dominio puede ser un conjunto a elección nuestra (ya que podemos escogerlo más pequeño o más grande) mientras que la imagen vendrá dada por el dominio escogido.A veces, pero, nos encontramos que nuestra función por ciertos motivos no puede ser evaluada en ciertos puntos ya que no está definida, así que tendremos que excluir ciertos puntos o intervalos del dominio.Ejemplo
Si tomamos la funciónf(x)=x+1x+1 podemos ver que cuandox=0 tenemos la expresión10 y esta división no puede realizarse.Por consiguiente, el dominio de esta función será todos los reales exceptuando el cero:Dom(f)=R∖{0}=(−∞,0)∪(0,∞) Y la imagen seráIm(f)=R∖{1}=(−∞,1)∪(1,∞) - Dominio de una función como el conjunto de valores donde evaluaremos la función. Se denota como:
- Mapa conceptual de funciones.
-
- Ejercicios de funciones.
-
- Gráficas de funciones. ( ejercicios)
-
-
 Q
Q








No hay comentarios:
Publicar un comentario